La transformée de Fourier

Savez-vous que presque tout peut être décomposé en une combinaison de fréquences (ondes sinusoidales) ?

Regardez par exemple ce dessin de Homer Simpson :

En combinant ensemble un nombre suffisant de fréquences (représentées dans cet exemple par une combinaison de cercles en rotation), le dessin est possible avec une grande précision.

Comment déterminer exactement combien de fréquences (y compris leur phase et amplitude) sont nécessaires pour créer le dessin ? La réponse est donnée mathématiquement par la transformée de Fourier.

Cette théorie permet de décomposer tout signal complexe en une somme de fréquences individuelles.

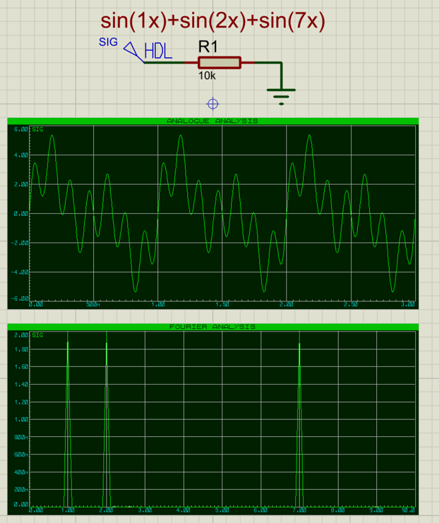
L’écran ci-dessus montre :

Un signal généré dans Proteus à l’aide d’un générateur à script;
Une représentation analogique de ce signal;
Une transformée de Fourier du signal décomposée en ses fréquences constitutives.

Ci-dessous une photo d’un analyseur de spectre numérique, qui peut être utilisé par exemple dans l’analyse des fréquences radios.

Les microcontrôleurs modernes, qui utilisent des instructions de traitement numérique du signal, peuvent analyser un signal analogique (numérisé avec un convertisseur anlogique-numérique – un CAN ou ADC) pour détecter et/ou filtrer certaines fréquences. L’avantage par rapport à des filtres analogiques et que le comportement peut être modifié à la volée par logiciel plutôt que de devoir changer les composants physiques.

La transformée de Fourier rapide

Mathématiquement, la transformée de Fourier calcule exactement la transformée d’une fonction depuis le domaine temporel vers le domaine fréquentiel. En pratique, un ingénieur électronique se sert d’un microcontrôleur pour caculer la transformée de Fourier d’un signal, uniquement avec une certaine résolution. Si le signal est lu avec un CAN (convertisseur analogique-numérique), ce calcul se fait à une cadence/résolution donnée.

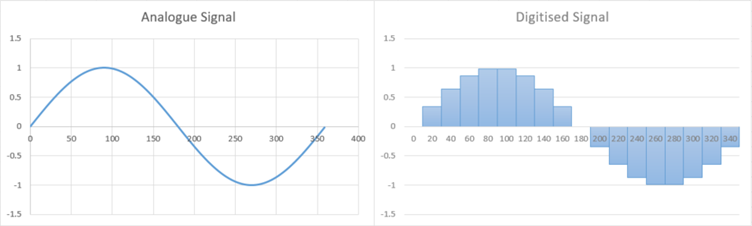
La transformée de Fourier rapide (FFT – Fast Fourier Transform) est une méthode efficace pour calculer la transformée de Fourier d’un signal échantillonné. Lors de la conception d’un système qui implique une FFT, il faut tenir compte d’une certain nombre de paramètres :

La fréquence d’échantillonnage;
Le nombre d’échantillons / la durée d’échantillonnage.

Fréquence d'échantillonnage

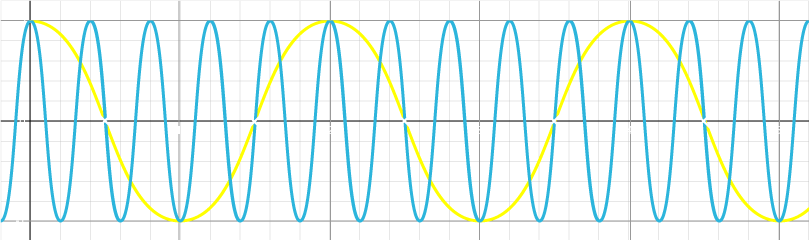
La fréquence d’échantillonnage, qui représente la cadence des données / le nombre de fois que le signal analogique est échantillonné (c.a.d. lu avec le CAN), déterminera la fréquence maximale que la FFT peut détecter. Voyons l’explication à ce problème connu sous le terme aliasing. Prenons les deux signaux qui suivent (jaune et bleu) :

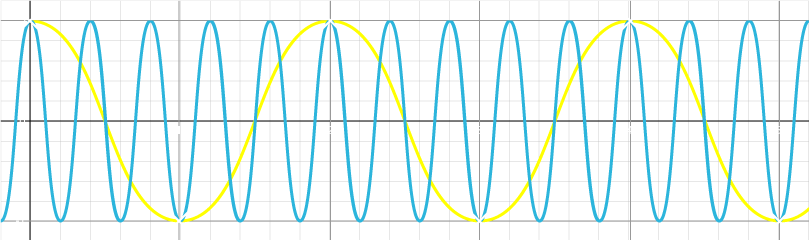
Si le signal jaune, à la fréquence de 2.5 Hz, est échantillonné à la fréquence de 1HZ, repéré par des croix (X) blanches, nous obtiendrons exactement les mêmes données que pour le même signal à 0.5Hz. La fréquence à laquelle le phénomène d’aliasing intervient est appelée fréquence de Nyquist. Elle est égale à la fréquence d’échantillonnage divisée par 2, donc pour l’exemple ci-dessus (échantillonnage à 1Hz), tout signal de fréquence 0.5Hz ou plus peut être perçu à une fréquence inférieure lors de la FFT. C’est un repliement de spectre.

Même le signal bleu de 0.5HZ, qui est égal à la fréquence de Nyquist dans notre cas, peut être vu à zéro s’il est échantillonné au mauvais moment.

Pour cette raison, il est important de valider une cadence d’échantillonage suffisament haute pour détecter la fréquence maximale qui doit être reçue par le système, et couper toutes les fréquences plus hautes avec un filtre analogique passe-bas si nécessaire.

Nombre d'échantillons

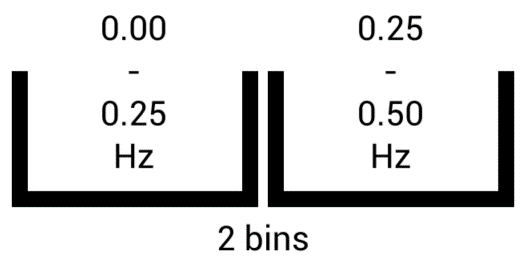
La seconde considération, est le nombre d’échantillons à acquérir, qui détermineront la résolution de la FFT. En fait, la FFT ne dit pas exactement quelles sont les fréquences présentes dans le signal, mais plutôt quelles sont les fréquences présentes dans un gamme de fréquences donnée. Si nous prenons uniquement 2 échantillons à 1 Hz par exemple, alors la FFT nous indiquera la force combinée des signaux dans la gamme 0.00Hz<->0.25Hz et la force combinée des signaux dans la gamme 0.25Hz<->0.50Hz. Le nombre de résultats produits par la FFT, aussi connu sous le terme ‘output bins’, est égale au nombre d’échantillons en entrée.

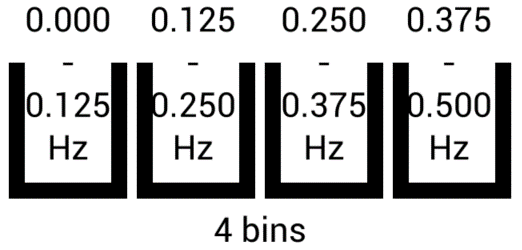
Le fait de passer à 4 bins / échantillons, doublera la résolution :

Bien sûr, nous pouvons en déduire qu’il faut prendre le plus d’échantillons possible, afin d’améliorer le résolution. Cependant tout dépend du temps de calcul et de la rapidité à laquelle nous voulons des résultats: si nous prenons 10 échantillons à 1 Hz, l’acquisition durera 10s – ou 60s si nous prenons 60 échantillons. Il faut donc tenir compte du temps de réaction du système pour déterminer le nombre d’échantillons à prendre. Une autre limitation est liée au temps de calcul de la FFT par le microcontrôleur – à quelle vitesse les données issues du CAN sont obtenues et la rapidité de traitement de la FFT.

Il est nécessaire de mentionner que l’aglorithme FFT, impose que le nombre d’échantillons / bins doit être une puissance de 2 pour que les calculs soient rapides – donc 2, 4, 8, 16, etc. La plupart des bibliothèques de calcul de FFT impose de disposer que le nombre d’échantillons soit une puissance de 2.

Le Goertzel

Si vous devez uniquement détecter la présence d’une fréquence particulière dans le signal, alors l’aglorithme de Goertzel est un moyen plus rapide. Le concept est le même pour la fréquence d’échantillonage et le nombre de bins, cependant le Goertzel ne calcule la valeur que pour un des bins.

Conclusion

La transformée de Fourier est un concept puissant utilisé de manière intensive en ingénierie. Sans être entré dans une description mathématique sur la théorie de la transformée de Fourier, nous avons présenté quelques considérations pratiques sur sa mise en oeuvre en utilisant une FFT.

Proteus inclut plusieurs outils et des exemples de projets de traitement numérique et analogique, y compris :

Simulation analogique, tel que le filtrage des signaux analogiques;
Génération de signal analogique; utilisation de générateurs interactifs ou par scripts;
Analyse de signal analogique; y compris analyse par Fourier et analyse fréquentielle;
DSP (Digital Signal Processing – traitement numérique du signal), simulation de microcontrôleur.

Traduction française