Communication I2C

Introduction

I2C (ou IIC) contraction de Inter-IC Communication, est un des plus populaires protocoles de communication implémenté sur les microcontrôleurs. Il est couramment utilisé pour interagir avec des capteurs mais se retrouve également dans beaucoup d’autres applications.

I2C est un protocole de communication synchrone, ce qui signifie qu’il existe une ligne horloge dédiée (voir les protocoles de communication synchrones/asynchrones).

Communication I2C

Bien que l’I2C n’utilise que deux lignes de communication (horloge et données), il peut prendre en charge plusieurs périphériques sur le même bus I2C. Cela est réalisé en utilisant un schéma d’adressage où chaque périphérique sur le bus a une adresse unique. La communication commence par l’envoi de l’adresse du périphérique avec lequel la communication est prévue, et le périphérique adressé doit ensuite accuser réception en indiquant qu’il est présent et prêt à communiquer.

Comme il n’y a qu’une seule ligne de données (SDA – données sérielles), utilisée à la fois pour l’envoi et la réception de données (mode half-duplex), un mécanisme est nécessaire pour permettre au maître et au périphérique esclave de contrôler la ligne de données sans conflits. Il est essentiel d’éviter les contentions sur le bus, où un périphérique tente d’écrire un niveau haut sur le bus tandis qu’un autre périphérique tente d’écrire un niveau bas sur le bus, ce qui créerait un court-circuit.

Pour y parvenir, on utilise un mécanisme open-drain ; où chaque périphérique ne peut mettre le bus qu’à un niveau « bas » ou le « relâcher », et des résistances de tirage sont utilisées pour ramener la ligne à un niveau haut lorsqu’elle est relâchée (si vous n’êtes pas familier avec les termes open-drain ou résistance de tirage, veuillez consulter notre article sur le sujet). La ligne d’horloge (SCL – Horloge sérielle) utilise également ce mécanisme, et quelques techniques innovantes sont utilisées pour ajouter des fonctionnalités utiles au protocole I2C – nous en parlerons plus en détail sous peu.

Le diagramme ci-dessous illustre les caractéristiques typiques d’une séquence de communication I2C.

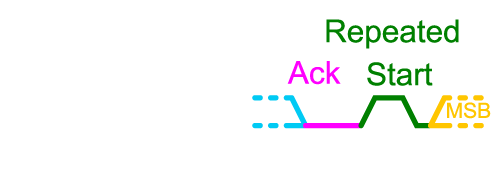
La communication débute avec le bus I2C en état de repos – les lignes d’horloge et de données ne sont pas activées et sont donc tirées vers le haut par les résistances de tirage. Ensuite, la communication est initiée par le maître (le périphérique initiant la communication) tirant d’abord la ligne SDA puis la ligne SCL vers le bas – cela est défini comme une condition de départ (Start).

Ensuite, le maître transmet l’adresse sur 7 bits du périphérique avec lequel il souhaite communiquer, suivie d’un bit « lire ou écrire » qui indique si le maître souhaite écrire (0) ou lire (1) à partir du périphérique. La ligne de données est considérée comme valide (lue par les esclaves) sur les fronts montants de la ligne d’horloge, et les données sont transmises en commençant par le bit le plus significatif (MSB).

Après que l’adresse a été transmise, et en supposant que l’esclave adressé est présent sur le bus I2C, le maître relâchera la ligne de données (open drain), et l’esclave maintiendra la ligne de données basse pendant un cycle d’horloge pour accuser réception (ack) qu’il est présent et prêt à communiquer. Si l’esclave n’est pas présent sur le bus, alors la résistance de tirage tirera la ligne de données vers le haut, et le maître saura que l’esclave n’est pas disponible.

À ce stade, les données peuvent être transmises entre le maître et l’esclave. Si des données sont lues, alors l’esclave transmettra les données (pendant que le maître continue de piloter la ligne d’horloge), ou si des données sont écrites, alors le maître transmettra les données. Après chaque octet de données, il y a un seul bit d’acquittement (Ack), pendant lequel le récepteur (qui peut être le maître ou l’esclave, selon le côté qui a transmis les données) doit maintenir la ligne de données basse pour indiquer qu’il a reçu la communication (et qu’il est prêt à passer à la communication suivante si nécessaire).

Etirement d'horloge

Les périphériques esclaves sur le bus I2C ont la capacité de retarder leurs réponses (s’ils sont toujours occupés et ne sont pas encore prêts à répondre) en maintenant la ligne d’horloge (SCL) à un niveau bas, une fonctionnalité connue sous le nom d’« étirement d’horloge » (clock stretching) ; une fois prêt à répondre, l’esclave relâche la ligne d’horloge et la transmission des données se poursuit. Ceci est similaire aux lignes de contrôle de flux dans l’UART (CTS/RTS), mais sans nécessiter de lignes de communication supplémentaires (notez que le protocole SPI n’a pas de fonction de contrôle de flux).

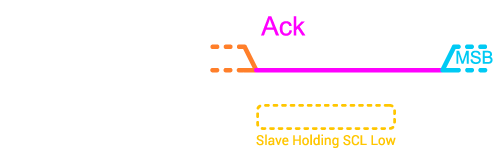
Un ou plusieurs octets de données peuvent être communiqués en séquence, avec un acquittement (ack) survenant après chaque octet.

Redémarrage

Parce que les périphériques esclaves peuvent avoir une multitude de valeurs disponibles à lire (telles que plusieurs valeurs de capteurs ainsi que des valeurs de réglages), l’esclave peut exiger que le maître émette d’abord une instruction indiquant ce qu’il souhaite lire avant de procéder à la lecture effective. Dans ce cas, le maître émettra d’abord une écriture avec les données indiquant ce qui doit être lu, puis le maître émettra immédiatement après une lecture. Cependant, il n’y a pas d’arrêt émis entre les deux. À la place, le maître utilise une condition de redémarrage (repeated start), suivie de l’adresse de 7 bits et du bit de lecture/écriture d’1 bit, maintenant réglé sur lecture, pour passer de l’écriture à la lecture. Pour émettre un redémarrage, le maître place d’abord la ligne de données à un niveau haut, puis la ligne d’horloge, et ensuite le maître abaisse la ligne de données suivie de la ligne d’horloge.

Débit et distances

La communication sur le bus I2C se déroule généralement à des vitesses de 100 kHz ou 400 kHz. Ces vitesses relativement basses conviennent bien pour de petites quantités de transmission de données, mais le SPI (utilisant des horloges dans la plage des mégahertz, et éventuellement en mode Dual ou Quad) est généralement préféré pour des applications à haut débit où de grandes quantités de données doivent être transmises. L’I2C est plutôt utilisé pour des communications sur des distances relativement courtes, cependant, des mécanismes existent permettant la transmission d’I2C sur des paires différentielles pour communiquer sur des distances plus longues (veuillez consulter notre article sur la conception à haut débit pour plus d’informations sur les paires différentielles).

Proteus inclut un instrument analyseur de protocole I2C en mode DUAL (maître ou esclave) à placer sur les liens du schéma. Cela vous permet ensuite de saisir et d’injecter des séquences I2C dans la simulation en cours et de visualiser les paquets reçus en provenance d’autres périphériques sur le bus I2C. C’est un excellent outil pédagogique qui permet un test rapide et facile des firmwares en mode maître et en mode esclave. Vous trouverez beaucoup d’exemples de projets qui incluent des communications I2C avec des capteurs ou des projets multi-processeurs. Tous ceux-ci peuvent être simulés dans la version de démonstration.

Article dont l’auteur est Dane du Plooy – eiTech Systems

Copyright Labcenter Electronics Ltd. 2024

Traduction française

Copyright Multipower France 2024

Visualisation 3D

Exploitez la Visualisation 3D dans Proteus : Du Concept à la Réalité

Les Larmes

Teardrops dans Proteus : Une Solution Essentielle pour la Durabilité des PCB

Filtres analogiques passifs

Dans le domaine du traitement numérique du signal, les filtres sont des éléments qui suppriment (ou, plus exactement atténuent) certaines fréquences contenues dans une forme d’onde.

Par exemple, prenons une fréquence basse de 1 KHz (amplitude 5V)

Et une fréquence plus rapide de 50KHz (amplitude 1V) :

Le signal combiné de ces deux fréquences ressemble à ceci :

Les générateurs de Proteus peuvent être initialisés en source de tension ou de courant. Pour sommer les deux générateurs de 1kHz et 50kHz nous les utilisons en source de courant comme montré ci-dessous relativement au signal sinusoidal de fréquence 50KHz!

Grâce à l’utilisation de filtres, nous pouvons décomposer le signal combiné, par filtrage, afin d’en extraire les différentes composants. Pourquoi faire cela ? Il existe de nombreuses raisons telles que :

Partager le medium

Dans le cas d’ondes radios (Wifi, téléphone mobile, etc) tous les signaux partagent le même canal de transmission. C’est comme s’il n’existait qu’un fil de communication partagé entre tous. Le fait d’utiliser des fréquences différentes, permet à plusieurs utilisateurs de partager le medium et de filtrer les fréquences pour ne s’intéresser qu’à certaines.

Medium partagé

2. Bruit

Le bruit peut être induit dans un signal par plusieurs sources, par exemple une interférence électromagnétique. Il est possible de supprimer ce bruit par filtrage.

Voyons comment nous implémentons des filtres.

Composants réactifs

Dit simplement, les composants réactifs sont des composants dont le comportement varie en fonction de la fréquence qui leur est appliquée. En électronique il existe deux types de composants réactifs, qui sont les condensateurs et les inductances. Les deux types de composants emmagasinent l’énergie dans un champ magnétique. Les condensateurs stockent l’énergie en accumulant des charges entre deux plaques.

Lorsqu’une tension est appliquée au condensateur alors un courant y circule jusqu’à ce que la tension entre les plaques corresponde à la tension appliquée. A ce stade, l’énergie est stockée dans les charges accumulées sur les plaques. Les charges sont maintenues en place grâce à l’attraction magnétique entre elles. Lorsque le condensateur est chargé, le courant s’arrête de circuler jusqu’à ce que la tension soit supprimée, ce qui permet au courant de circuler à nouveau.

Ainsi nous voyons que le courant circule lorsque la tension évolue et s’arrête de circuler lorsque la tension est constante ; lorsqu’il n’y a pas de différence de tension, aucun courant ne circule. Il semble contre intuitif qu’un courant puisse circuler dans un condensateur en mode DC, car il n’y a pas de connexion entre les plaques du condensateur ; cependant un courant AC peut y circuler car l’énergie est transférée via le champ magnétique interne au condensateur. Dans une optique AC, le condensateur bloque les basses fréquences alors que les hautes fréquences peuvent circuler.

Aux basses fréquences, le condensateur ressemble à un circuit ouvert. Aux fréquences hautes, le condensateur est un court-circuit. Entre les deux, le condensateur est équivalent à une résistance qui s’oppose au passage du courant. La spécificité d’un condensateur, c’est qu’il ne dissipe pas l’énergie en chaleur comme une résistance, mais la stocke dans son champ magnétique.

Les inductances, quant à elles, stockent l’énergie dans le champ magnétique qui se développe autour des spires.

Contrairement aux condensateurs, les inductances permettent au courant d’y circuler lorsque la tension ne change pas, et s’opposent à des changements de courant et de tension. Alors que les condensateurs ressemblent plus à un élastique, les inductances font penser à une roue libre (voir les articles sur les convertisseurs ‘boost’ et ‘buck’). Lorsqu’une tension est appliquée à une inductance, initialement elle s’oppose à la circulation de courant pendant l’établissement d’un champ magnétique autour de ses spires. Une fois établi, le courant DC traverse l’inductance sans entrave. Si vous tentez d’arrêter le passage du courant, alors le champ magnétique produit une tension qui tente de préserver la circulation du courant.

Aux basses fréquences, le condensateur ressemble à un court-circuit. Aux fréquences hautes, le condensateur est comparable à un circuit ouvert. Entre les deux, une inductance est équivalente à une résistance qui s’oppose au passage du courant. La spécificité d’une inductance, c’est qu’elle ne dissipe pas l’énergie en chaleur comme une résistance, mais la stocke dans son champ magnétique.

Avec les condensateurs et les inductances, nous disposons de deux éléments réactifs, de comportement opposé par rapport à des fréquences AC. Nous pouvons utiliser ces propriétés pour construire des filtres avec ces composants.

Décibels

Avant d’aller plus loin, il est important de comprendre l’unité de mesure appelée décibel. C’est une unité logarithmique illustrée dans le graphe qui suit :

20dB signifie 10 x l’amplitude et 100 x la puissance, 40dB signifie 100 x l’amplitude et 10000 x la puissance, et ainsi de suite (nous n’indiquerons par ici la relation entre l’amplitude AC et la puissance AC).

Il suffit de dire que le calcul de la puissance AC est plus complexe que la puissance DC donnée par P = V x I. Les décibels (dB) sont une unité de mesure qui nous permet de travailler facilement depuis de très faibles valeurs vers des très grandes, et rend les calculs très simples pour une chaîne de systèmes car les dBs s’additionnent.

Graphe de réponse en fréquence

Le graphe de réponse en fréquence ou diagramme de Bode montre la réponse d’un circuit en fonction de la fréquence. Il est donc particulièrement adapté à la conception et l’analyse des filtres comme nous allons le voir dans les prochaines sections.

Le filtre passe-haut

Ce filtre permet aux fréquences hautes de le traverser, alors que les basse fréquences sont atténuées (bloquées). Comme nous l’avons vu, les condensateurs admettent les hautes fréquences, c’est pourquoi nous utiliserons ces composants pour construire un filtre passe-haut.

Le graphe de réponse en fréquence montre que les fréquences supérieures à 16k sont admises (proches de 0dB), alors que les fréquences plus basses sont atténuées de plus en plus (à 100 Hz, l’atténuation est de -44 dB) . Le filtre n’est pas un mur de brique qui bloque toutes les fréquences mais plutôt les atténue de plus en plus lorsque la fréquence diminue. Nous pouvons augmenter l’atténuation en combinant des filtres, ce qui augmente l’ordre du filtre.

Super ! Essayons cela avec notre exemple initial :

Nous voyons que la fréquence de 1 KHz est pratiquement éliminée du signal après le condensateur (courbe rouge du graphe). Nous verrons plus loin comment calculer la valeur des composants pour une fréquence donnée.

Le filtre passe-bas

Le filtre passe-bas est l’opposé du filtre passe-haut et permet aux fréquence basses de passer tout en atténuant les fréquences hautes. Pour modifier notre exemple, il suffit de remplacer le condensateur par une inductance :

Dans ce cas, la fréquence haute de 50 kHz est pratiquement supprimée du signal après la passage par l’inductance (courbe rouge du graphe). Le graphe de réponse en fréquence pour l’inductance ressemble à celui-ci :

Les fréquences plus basses que 3k passent (proche de 0dB) alors que les fréquences supérieures sont de plus en plus atténuées (à 100kHz, l’atténuation est de -30dB). Ici aussi, il est possible de combiner des filtres pour améliorer l’atténuation.

Nous pouvons aussi construire un filtre passe-bas avec un condensateur :

Dans ce cas les hautes fréquences passent au travers le condensateur vers la masse. Le graphe correspondant ressemble à ceci :

Autre filtre passe-haut

De la même manière nous pouvons construire un filtre passe-haut avec une inductance :

Dans ce cas, ce sont les basses fréquences qui traversent l’inductance vers la masse. Le graphe correspondant ressemble à ceci :

La fréquence de coupure

La fréquence de coupure correspond au point à – 3dB du graphe de réponse en fréquence. C’est le point pour lequel le signal est atténué de 50% par rapport à la puissance d’origine (approximativement 70.8% de la tension d’origine). C’est aussi le point de rencontre des lignes d’atténuation de de passage du signal.

La fréquence de coupure est donnée par la formule :

Cutoff Frequency = 1 / 2πRC

pour un filtre capacitif. Pour un filtre inductif, c’est :

Cutoff Frequency = R / 2πL

Utilisons ces formules avec la valeur des composants de nos graphes de réponse plus haut. Dans le cas du filtre capacitif, nous avons une résistance de 10k avec un condensateur de 1nF, ce qui donne :

Cutoff Frequency = 1/2π(10×10³)(1×10-9) = 15.9kHz

Pour le filtre inductif, nous avons une résistance de 10k avec une inductance de 100mH :

Cutoff Frequency = (10×10³)/2π(0.1) = 15.9kHz

Dans le deux cas, nous voyons que les valeurs correspondent à celles de graphes.

Filtres d’ordre plus élevés

Tous les filtres que nous avons présenté contiennent un seul élément réactif. La pente des graphes de réponse est d’environ 10dB/décade logarithmique. En utilisant plus d’éléments réactifs et/ou en associant des filtres nous pouvons augmenter la pente de 20dB par élément réactif. On dit que l’ordre du filtre augmente. Par exemple, ci-dessous nous présentons un filtre du deuxième ordre (2 éléments réactifs) avec une pente de 40dB/décade.

Notez cependant qu’il y existe des inconvénients à trop incrémenter l’ordre du filtre car cela fait varier l’atténuation du signal dans la bande passante et ajoute un retard de propagation. De plus la complexité du circuit augmente ainsi que son coût.

Filtres passe-bande et coupe-bande

Il est également possible de créer des filtres passe-bande ou coupe-bande par une combinaison de filtre passe-haut et passe-bas avec des fréquences de coupure appropriées.

Conclusion

Les filtres sont des modules assez simples à comprendre et représentent des outils essentiels en traitement du signal, à connaître par tout ingénieur. Dans cet article nous nous sommes concentrés sur la filtres analogiques passifs ; il existe également des filtres analogiques actifs que nous aborderons dans un autre article.

Tous les exemples et les graphes de cet article ont été créés avec la suite Proteus. Le module de simulation avancée par graphes dispose de douze types de graphes différents avec la possibilité d’inclure des générateurs de signaux ainsi que des sondes de tension/courant.

Copyright Labcenter Electronics Ltd. 2024

Traduction française

Copyright Multipower France 2024

La transformée de Fourier

Savez-vous que presque tout peut être décomposé en une combinaison de fréquences (ondes sinusoidales) ?

Regardez par exemple ce dessin de Homer Simpson :

En combinant ensemble un nombre suffisant de fréquences (représentées dans cet exemple par une combinaison de cercles en rotation), le dessin est possible avec une grande précision.

Comment déterminer exactement combien de fréquences (y compris leur phase et amplitude) sont nécessaires pour créer le dessin ? La réponse est donnée mathématiquement par la transformée de Fourier.

Cette théorie permet de décomposer tout signal complexe en une somme de fréquences individuelles.

L’écran ci-dessus montre :

Un signal généré dans Proteus à l’aide d’un générateur à script;
Une représentation analogique de ce signal;
Une transformée de Fourier du signal décomposée en ses fréquences constitutives.

Ci-dessous une photo d’un analyseur de spectre numérique, qui peut être utilisé par exemple dans l’analyse des fréquences radios.

Les microcontrôleurs modernes, qui utilisent des instructions de traitement numérique du signal, peuvent analyser un signal analogique (numérisé avec un convertisseur anlogique-numérique – un CAN ou ADC) pour détecter et/ou filtrer certaines fréquences. L’avantage par rapport à des filtres analogiques et que le comportement peut être modifié à la volée par logiciel plutôt que de devoir changer les composants physiques.

La transformée de Fourier rapide

Mathématiquement, la transformée de Fourier calcule exactement la transformée d’une fonction depuis le domaine temporel vers le domaine fréquentiel. En pratique, un ingénieur électronique se sert d’un microcontrôleur pour caculer la transformée de Fourier d’un signal, uniquement avec une certaine résolution. Si le signal est lu avec un CAN (convertisseur analogique-numérique), ce calcul se fait à une cadence/résolution donnée.

La transformée de Fourier rapide (FFT – Fast Fourier Transform) est une méthode efficace pour calculer la transformée de Fourier d’un signal échantillonné. Lors de la conception d’un système qui implique une FFT, il faut tenir compte d’une certain nombre de paramètres :

La fréquence d’échantillonnage;
Le nombre d’échantillons / la durée d’échantillonnage.

Fréquence d'échantillonnage

La fréquence d’échantillonnage, qui représente la cadence des données / le nombre de fois que le signal analogique est échantillonné (c.a.d. lu avec le CAN), déterminera la fréquence maximale que la FFT peut détecter. Voyons l’explication à ce problème connu sous le terme aliasing. Prenons les deux signaux qui suivent (jaune et bleu) :

Si le signal jaune, à la fréquence de 2.5 Hz, est échantillonné à la fréquence de 1HZ, repéré par des croix (X) blanches, nous obtiendrons exactement les mêmes données que pour le même signal à 0.5Hz. La fréquence à laquelle le phénomène d’aliasing intervient est appelée fréquence de Nyquist. Elle est égale à la fréquence d’échantillonnage divisée par 2, donc pour l’exemple ci-dessus (échantillonnage à 1Hz), tout signal de fréquence 0.5Hz ou plus peut être perçu à une fréquence inférieure lors de la FFT. C’est un repliement de spectre.

Même le signal bleu de 0.5HZ, qui est égal à la fréquence de Nyquist dans notre cas, peut être vu à zéro s’il est échantillonné au mauvais moment.

Pour cette raison, il est important de valider une cadence d’échantillonage suffisament haute pour détecter la fréquence maximale qui doit être reçue par le système, et couper toutes les fréquences plus hautes avec un filtre analogique passe-bas si nécessaire.

Nombre d'échantillons

La seconde considération, est le nombre d’échantillons à acquérir, qui détermineront la résolution de la FFT. En fait, la FFT ne dit pas exactement quelles sont les fréquences présentes dans le signal, mais plutôt quelles sont les fréquences présentes dans un gamme de fréquences donnée. Si nous prenons uniquement 2 échantillons à 1 Hz par exemple, alors la FFT nous indiquera la force combinée des signaux dans la gamme 0.00Hz<->0.25Hz et la force combinée des signaux dans la gamme 0.25Hz<->0.50Hz. Le nombre de résultats produits par la FFT, aussi connu sous le terme ‘output bins’, est égale au nombre d’échantillons en entrée.

Le fait de passer à 4 bins / échantillons, doublera la résolution :

Bien sûr, nous pouvons en déduire qu’il faut prendre le plus d’échantillons possible, afin d’améliorer le résolution. Cependant tout dépend du temps de calcul et de la rapidité à laquelle nous voulons des résultats: si nous prenons 10 échantillons à 1 Hz, l’acquisition durera 10s – ou 60s si nous prenons 60 échantillons. Il faut donc tenir compte du temps de réaction du système pour déterminer le nombre d’échantillons à prendre. Une autre limitation est liée au temps de calcul de la FFT par le microcontrôleur – à quelle vitesse les données issues du CAN sont obtenues et la rapidité de traitement de la FFT.

Il est nécessaire de mentionner que l’aglorithme FFT, impose que le nombre d’échantillons / bins doit être une puissance de 2 pour que les calculs soient rapides – donc 2, 4, 8, 16, etc. La plupart des bibliothèques de calcul de FFT impose de disposer que le nombre d’échantillons soit une puissance de 2.

Le Goertzel

Si vous devez uniquement détecter la présence d’une fréquence particulière dans le signal, alors l’aglorithme de Goertzel est un moyen plus rapide. Le concept est le même pour la fréquence d’échantillonage et le nombre de bins, cependant le Goertzel ne calcule la valeur que pour un des bins.

Conclusion

La transformée de Fourier est un concept puissant utilisé de manière intensive en ingénierie. Sans être entré dans une description mathématique sur la théorie de la transformée de Fourier, nous avons présenté quelques considérations pratiques sur sa mise en oeuvre en utilisant une FFT.

Proteus inclut plusieurs outils et des exemples de projets de traitement numérique et analogique, y compris :

Simulation analogique, tel que le filtrage des signaux analogiques;
Génération de signal analogique; utilisation de générateurs interactifs ou par scripts;
Analyse de signal analogique; y compris analyse par Fourier et analyse fréquentielle;
DSP (Digital Signal Processing – traitement numérique du signal), simulation de microcontrôleur.

Traduction française

Couture et blindage du PCB avec des vias

La couture de vias sur le PCB consiste à utiliser un grand nombre de vias pour connecter es zones de cuivre placées sur différentes couches. Le blindage par des vias (aussi appelé ”picket fence » en anglais) consiste à utiliser une ou deux rangées de vias placées en périphérie des pistes pour relier des zones de cuivre. Il existe de nombreux points de vue différents sur quand et comment utiliser les vias de couture/blindage sur votre PCB, dont nous allons résumer certains dans cet article.

Masse constante

L’utilisation la plus courante de la couture avec des vias est probablement de garantir des chemins de retour courts pour les signaux ou d’aider à maintenir une masse constante. Dès qu’un courant commence à circuler, il induit une tension sur le cuivre qu’il traverse, ce qui permet à la fois de répartir le courant et de faire “rebondir” la masse en fonction de la partie du PCB concernée. La couture par vias peut être un moyen efficace et peu coûteux de stabiliser la masse sur le PCB.

Gestion de la chaleur

Sur certains PCBs, la couture de vias peut être utile pour mieux distribuer la chaleur. Un PCB est plus conducteur horizontalement (le long de la couche) que verticalement (traversée de la carte). Si le suivi n’est effectué que sur les couches extérieures, une grande partie de la chaleur est transportée latéralement et le noyau peut être plus froid que les pistes. En cousant cette construction avec des vias, on améliore la conductivité, ce qui permet de dissiper la chaleur, réduisant ainsi les températures globales. Cet avantage disparaît bien sûr si toute la carte est utilisée pour transporter du courant et qu’il n’y a donc pas d’endroit plus froid où la chaleur peut se répandre.

Diaphonie

Relier le cuivre par couture peut également être utilisé pour réduire le couplage capacitif entre les signaux. Représentez-vous les pistes adjacentes du circuit comme les terminaux d’un condensateur, l’espace qui les sépare étant le diélectrique. Plus l’espace est important, moins la capacitance sera importante ainsi que la diaphonie. La couture par cuivre entre des pistes aura le même effet d’un espacement plus petit (plus de diaphonie!) sauf si le cuivre est correctement mis à la masse. Il est donc important d’être certain que la couture par cuivre est effective à la fréquence d’intérêt. Dans ce rôle, la couture par vias tend à être utilisée dans le cas d’une haute impédance, d’un circuit analogique (ADCs, SMPS, etc) lorsqu’il manque un bon plan de référence.

CEM

La couture par cuivre autour des pistes à hautes fréquences est réalisée pour différentes raisons. Le but est d’enfermer les ondes électromagnétiques rayonnées par ces pistes. Malheureusement, les isolants – y compris le noyau diélectrique FR4 du ¨CB – sont de bons conducteurs d’ondes électromagnétiques. Lorsque la fréquences des signaux augmente pour atteindre une longueur d’onde comparable à la taille des éléments de cuivre sur le PCB, les deux plans de masse deviennent des guides d’ondes qui font rebondir les ondes entre elles jusqu’à trouver la sortie par le côté du circuit. La pratique admise est de coudre/blinder les plans de masse d’une carte RF avec des vias espacés au minimum de 1/10ème de la plus haute fréquence d’intérêt. L’objectif est de conserver, sur le substrat du diélectrique, un espacement suffisamment petit en comparaison de la longueur d’onde afin que la couture apparaisse comme continue par rapport aux ondes incidentes.

Equilibre du cuivre

Pour terminer, la couture des plans entre eux peut présenter des avantages lors de la fabrication du circuit car les vias pourrait relier des zones de cuivre non connectées (ilots) au net, ce qui permet d’augmenter la couverture de cuivre. Globalement, le résultat est que le PCB aura des quantités plus équilibrées de cuivre de chaque côté du circuit, ce qui peut aider à prévenir la déformation pendant la refusion.

Appliquer la commande de couture

La plupart des CAOs proposent des mécanismes pour coudre automatiquement deux zones de cuivre entre elles. La première décision pour le concepteur est d’inclure ou pas les ilots dans la propagation du cuivre. Un ilot est une zone de cuivre qui n’a pas de connexion au net sur sa couche mais qui en obtiendra une par couture à une autre zone de cuivre. Dans Proteus, la case à cocher ‘supprimer les ilots’ est utilisée pour contrôler la diffusion du cuivre lorsque vous placez un plan de masse

Lorsque les surfaces à remplir sont définies sur les deux couches, l’utilisateur appelle la commende de couture par traversées. Une boite de dialogue de configuration autorise le choix du style de via, de la distance minimale d’isolement à respecter entre les vias et le logiciel en tiendra compte lors du placement des vias. Une fois configurée, cette commande suture généralement la surface commune des deux plans de masse

Bien que cela soit évident, l’erreur la plus courante est de coudre les plans entre eux trop tôt pendant la conception du circuit. Un PCB qui contient trop de coutures rendra le routage plus compliqué; il est donc préférable d’effectuer le routage en premier.

Appliquer la commande de blindage

Les vias de blindage, parfois appelés ‘via fences’ ou ‘picket fences’, suivent les mêmes principes que les vias de couture, mais consistent généralement en une seule rangée de traversées placées autour des pistes ou des limites de la coulée de cuivre. Ils sont presque toujours utilisés pour isoler les zones de la carte qui fonctionnent à des fréquences différentes et pour le contrôle des interférences électromagnétiques, comme indiqué ci-dessus.

De manière procédurale, vous appliquerez les vias de blindage presque de la même manière. Vous pouvez sélectionner soit la ou les pistes à blinder, soit le plan de masse si les vias sont appliqués au périmètre de la coulée de cuivre. La boite de dialogue de blindage des traversées est alors lancée à partir du menu contextuel et la configuration s’effectue de la même manière que pour la couture de vias.

Résumé

La question de savoir s’il est nécessaire ou non de suturer votre cuivre est souvent débattue par les concepteurs de PCB. La réponse n’est pas évidente car elle suppose une grande expérience pratique en ce domaine. Cependant, cet article indique les principales problématiques associées à ces techniques.

Traduction française