Une introduction aux filtres actifs
Introduction
Cet article est la suite des articles sur les filtres passifset les amplificateurs opérationnels.
Les filtres actifs ajoutent des éléments actifs dans la circuiterie du filtre ; des éléments actifs sont des composants qui sont alimentés séparément plutôt que par le signal lui-même. L’ajout d’un amplificateur tampon (buffer) après le filtre permet de piloter des charges plus importantes avec le signal sans atténuation, tel que le filtre passe-haut de l’exemple ci-dessous :
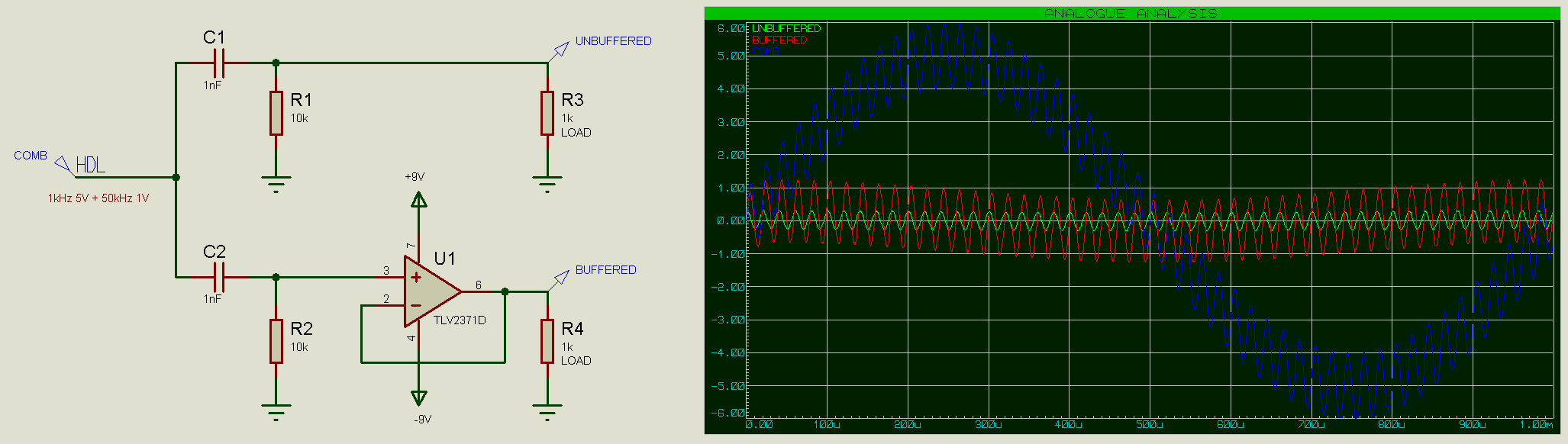
Notez que la sortie sans buffer (courbe verte) est atténuée de manière significative par rapport à la sortie avec buffer (courbe rouge).
Pourquoi utiliser des composants actifs
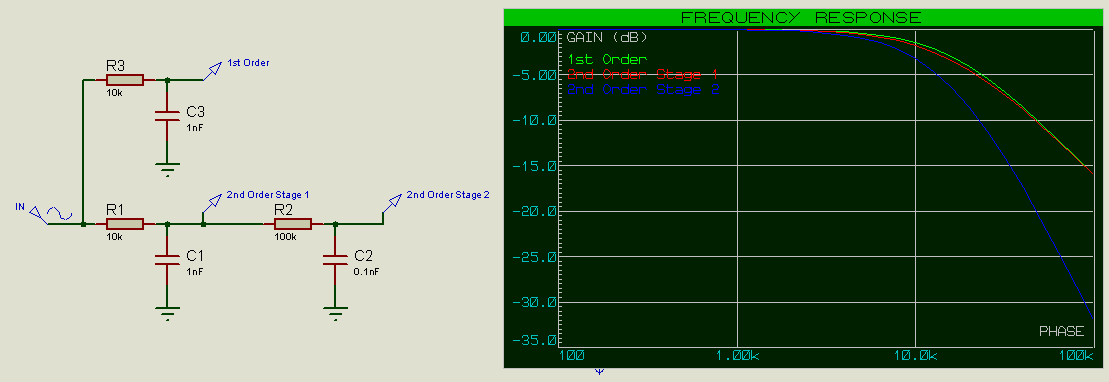
Le fait d’ajouter des buffers dans une chaîne de filtres passe-haut d’ordre élevé permet de réduire l’atténuation entre chaque lien de la chaîne et évite les distorsions des caractéristiques du filtre global liés aux éléments de chaque filtre de la chaîne. Par exemple, regardons le comportement d’un filtre passe-bas d’ordre 2, pour constater que l’élément résistif vu par le second filtre n’est pas juste R2=10k mais R1+R2=20k et que la capacitance vue par le premier filtre n’est pas juste C1 car la capacitance de C2 doit être prise en compte également.
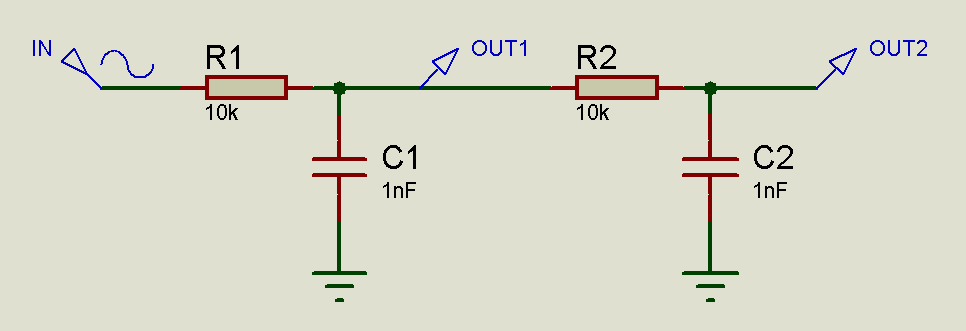
Étant donné que
Cutoff Frequency = 1/2πRC
Ceci a pour effet de décroitre la fréquence de coupure du filtre.
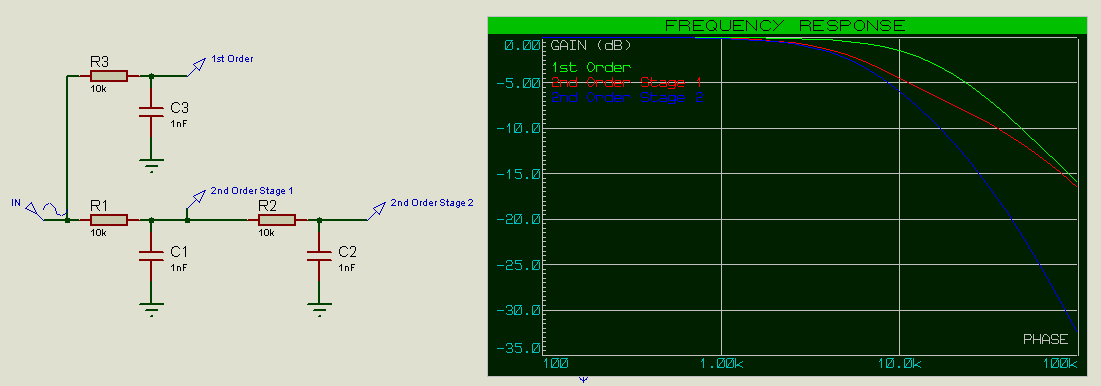
Pour R=10k et C=1nF, nous nous attendons à ce que la fréquence de coupure soit de 15,9KHz (-3dB pour le premier étage du filtre et -6dB pour le second). Cependant nous observons que la valeur est plus basse que cela. Notez comment la réponse en fréquence notée « 2nd order stage 1 » suit celle de « 2nd order stage 2 », car aux basses fréquences les condensateurs se comportent comme des circuits ouverts (comme s’ils n’étaient pas là). Cependant aux hautes fréquences la réponse en fréquence de « 2nd order stage 1 » suit celle du filtre « 1st order » car C1 commence à se comporter comme un court-circuit avec une faible résistance par comparaison avec R2.
L’effet est plus prononcé si nous diminuons la résistance et augmentons la capacitance (pour un RC constant) dans le second étage du filtre.
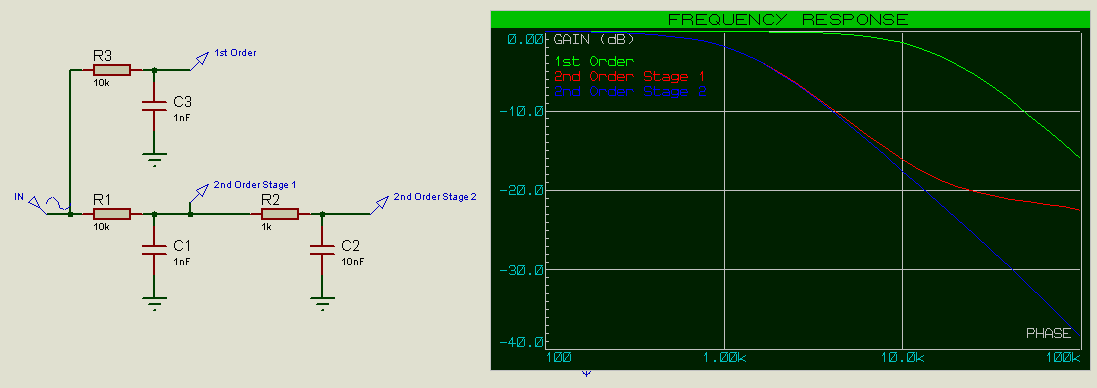
Ceci décale la fréquence de coupure encore plus bas.
Une façon de limiter cela est d’avoir une impédance d’entrée du second étage au moins égale à 10x celle de sortie du premier étage – c.a.d. R2 dix fois plus grande que R1 (et C2 10x plus petit, pour conserver un RC constant).
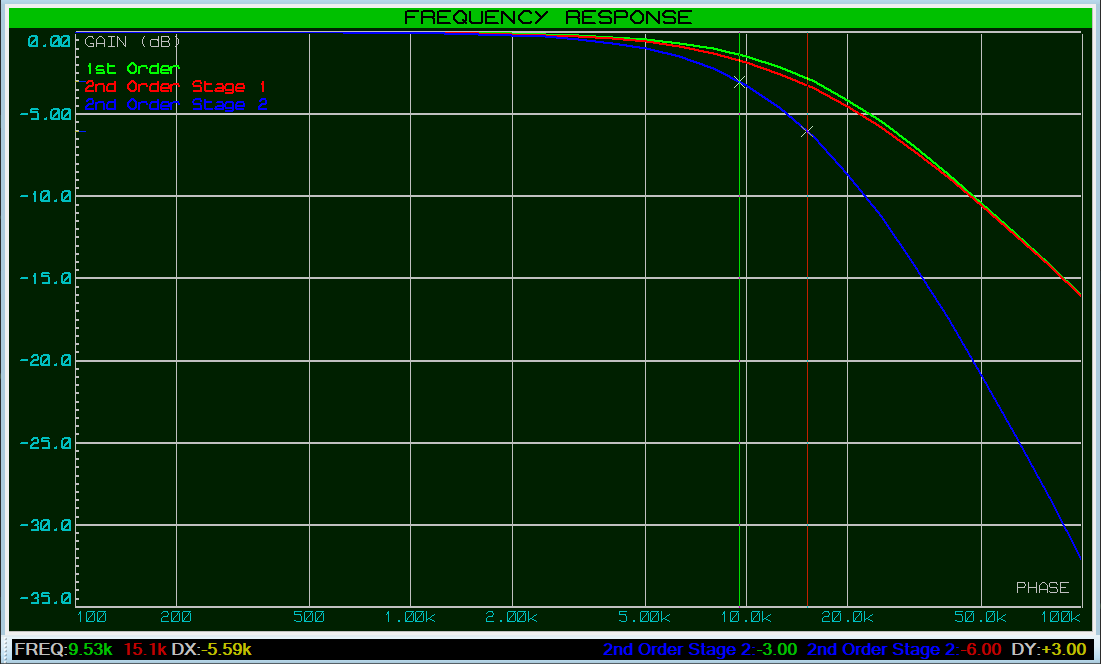
A présent nous voyons que la réponse en fréquence du premier étage du filtre du deuxième ordre se rapproche de celle du filtre du premier ordre.
La fréquence de coupure est également plus proche de celle attendue de 15,9kHz.
Plus on décroit l’impédance de sortie du premier étage et/ou on augmente l’impédance de sortie du deuxième étage, plus on se rapproche de la fréquence de coupure attendue mais sans l’atteindre exactement. Ajouter un troisième (ou quatrième) étage de filtre compliquerait encore plus la situation.
Voilà pourquoi nous introduisons des composants actifs !
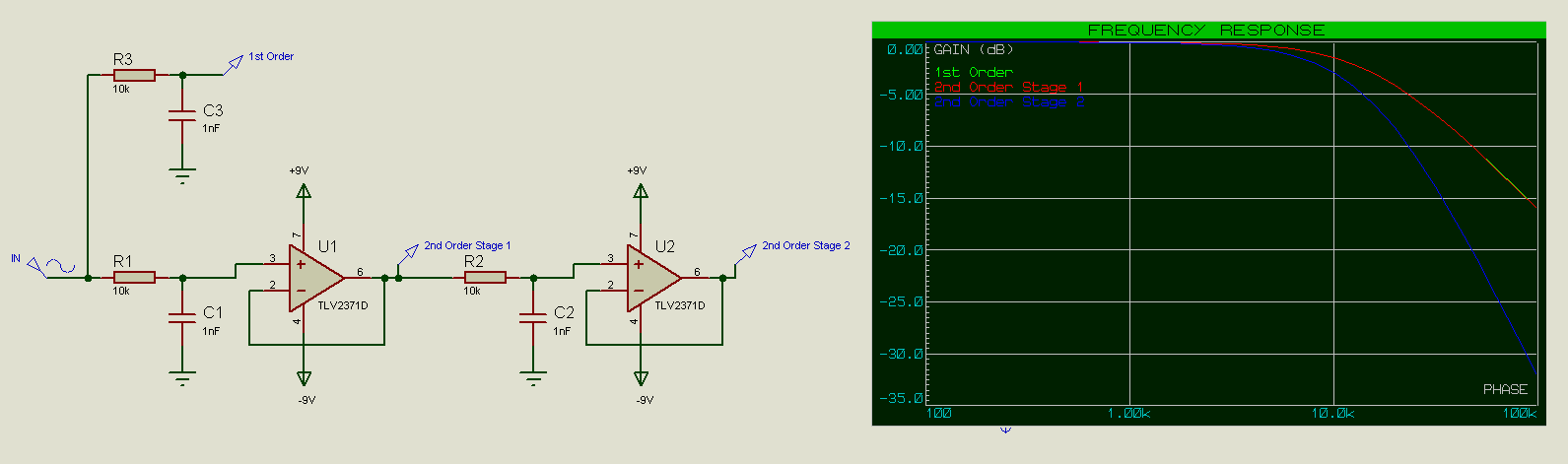
Dans ce cas nous voyons que le premier étage du filtre du second ordre correspond exactement au filtre du premier ordre et la fréquence de coupure est de 15,9kHz.
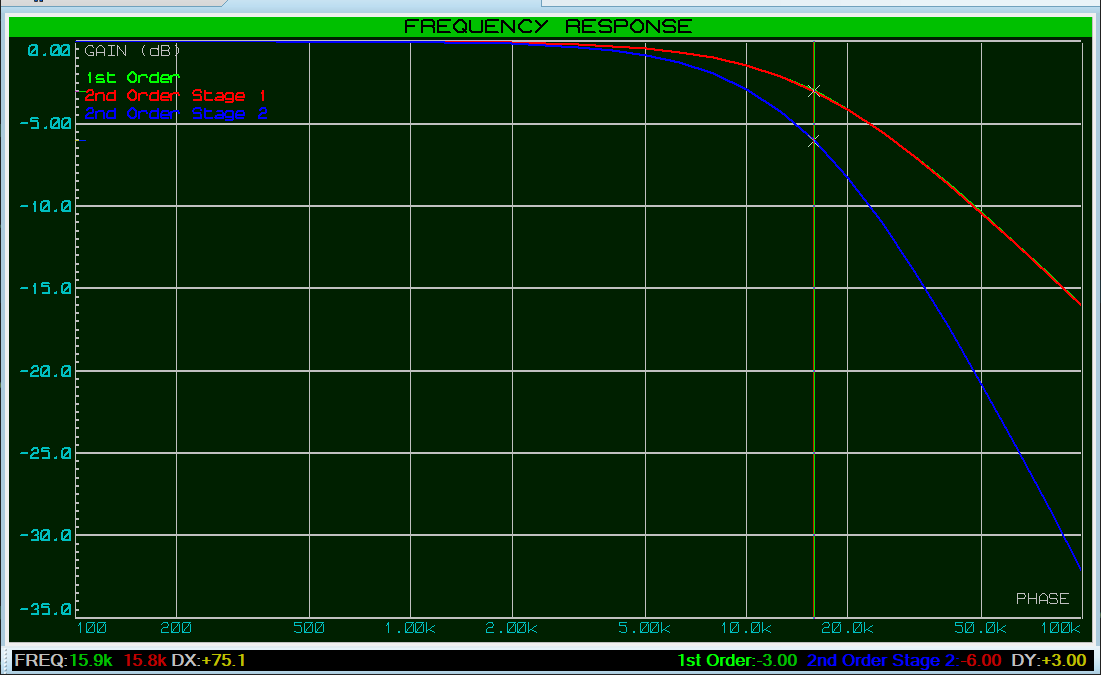
Nous pouvons aisément ajouter des étages de filtre pour obtenir une pente plus importante.
Notez que l’atténuation en dB à la fréquence de coupure augmente de -3dB pour chaque étage filtre supplémentaire. Un filtre du premier ordre aura une atténuation de –3dB à la fréquence de coupure, un filtre d’ordre 2 de -6dB, un filtre d’ordre 3 de -6dB, etc.
Topologie Sallen-Key
La topologie Sallen-Key est une topologie populaire de filtre du second ordre qui utilise un seul amplificateur opérationnel (au lieu de 2 dans notre exemple plus haut).
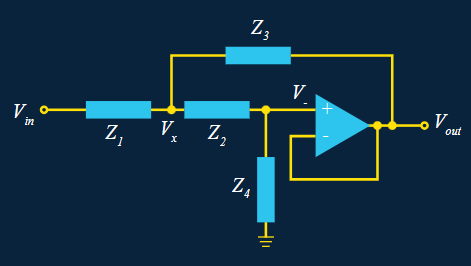
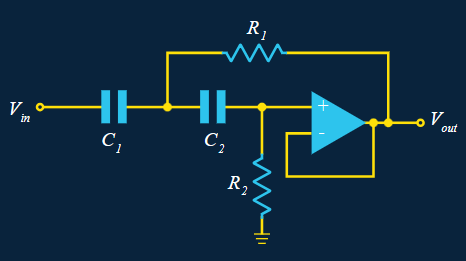
Un gain peut être ajouté en option (en utilisant un diviseur de tension sur l’entrée inverseuse de l’ampli op) :
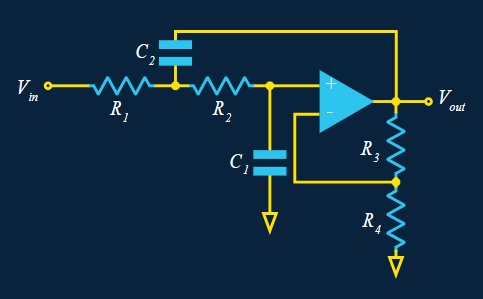
La caractéristique intéressante du filtre Sallen-Key est que le premier étage est connectée non pas à la masse mais plutôt à la sortie de l’ampli op. Ceci ajoute un retour (feedback) de la sortie de l’ampli op sur l’entrée positive, qui peut être utilisée pour augmenter le « Q » du filtre.
Le facteur de qualité, Q
En science, le facteur de qualité d’un système oscillant décrit son amortissement. Un pendule qui se balance dans l’air a un facteur de qualité supérieur à un pendule qui se balance dans l’eau ; le pendule dans l’air perd moins d’énergie entre chaque oscillation car il rencontre moins de résistance.
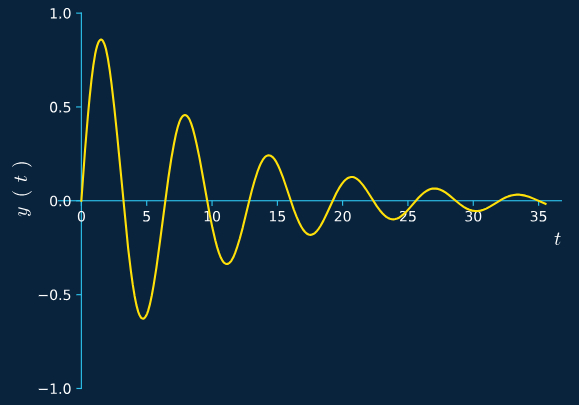
- Q=1 signifie qu’il n’y a pas d’amortissement et que l’amplitude du signal reste constante.
- Q >1 signifie que le signal est amplifié.
- Q<1 signifie que le signal est atténué.
En termes de réponse du filtre, le Q d’un filtre décrit comment il se comporte autour de la fréquence de coupure (10kHz dans le graphe ci-dessous) :
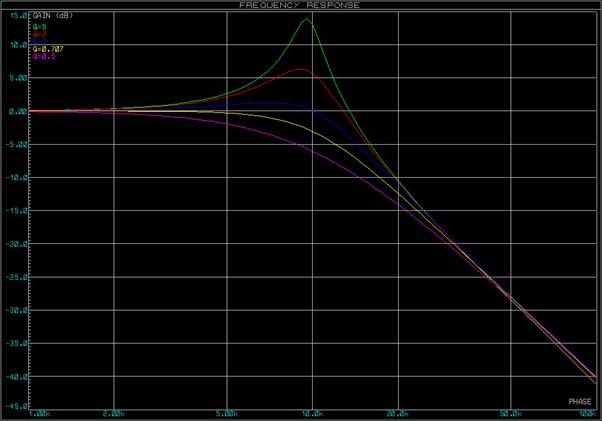
- Q > 1 amplifiera le signal à la fréquence ce coupure.
- Q = 1 conservera la même amplitude au signal à la fréquence de coupure.
- Q < 1 atténuera le signal à la fréquence de coupure.
Notez également que des valeurs Q plus grandes impliquent des angles plus prononcés à la fréquence de coupure. Un filtre passif du premier ordre aura un Q de 0,707 (-3dB) et un filtre du deuxième ordre un Q de 0,5 (-6dB). Si nous utilisons une topologie active Sallen-Key, nous pouvons choisir la valeur de Q.
Cela fonctionne de la façon suivante : le signal filtré à la sortie et renvoyé sur l’entrée, pour résonner avec lui autour de la fréquence de coupure et ainsi augmenter l’amplitude (donc le Q).
Calculs passe-bas
Les mathématiques liées au filtres Sallen-Key sont complexes et leur analyse dépasse le cadre de cet article. Il existe des calculateurs en ligne ou hors ligne pour déterminer aisément les valeurs R et C en relation avec une fréquence de coupure, un Q et un gain donnés. Cependant, nous allons jeter un coup d’œil à un cas simple où le gain vaut 1 et la valeur des résistances et des condensateurs sont des ratios les uns des autres.
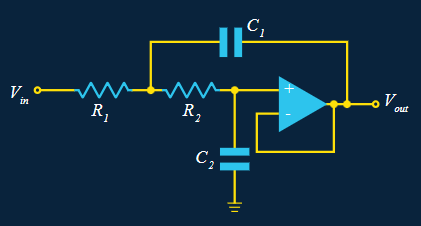
Let R2 = xR1, and C2=(1/x)C1.
C’est similaire à ce que nous avons fait précédemment (lorsque nous avons créé un filtre passif à 2 étages qui atténue les effets sur la fréquence de coupure) et la formule de calcul de la fréquence de coupure est toujours de 1 / 2πRC.
The formula for Q is then x / (x + 1).
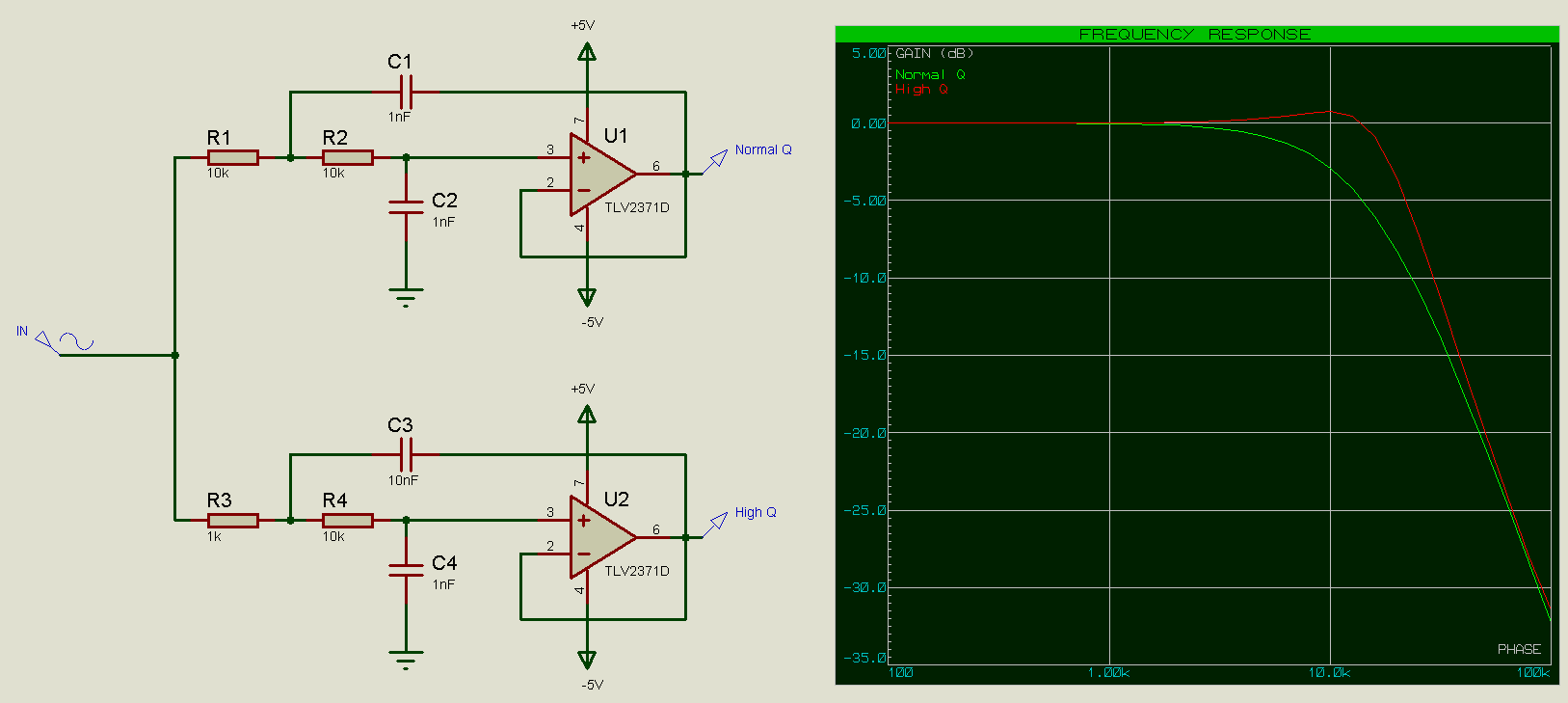
Nous voyons que si x=1 (les composants des deux étages sont les mêmes) alors nous obtenons un Q de 1 / (1 + 1) = 1/2 = 0,5 ; c’est un Q identique au cas usuel de filtre à 2 étages (-6dB). Si nous augmentons x à 10 nous aurons un Q de 10/11 = 0,91 bien supérieur à ce que nous avions précédemment.
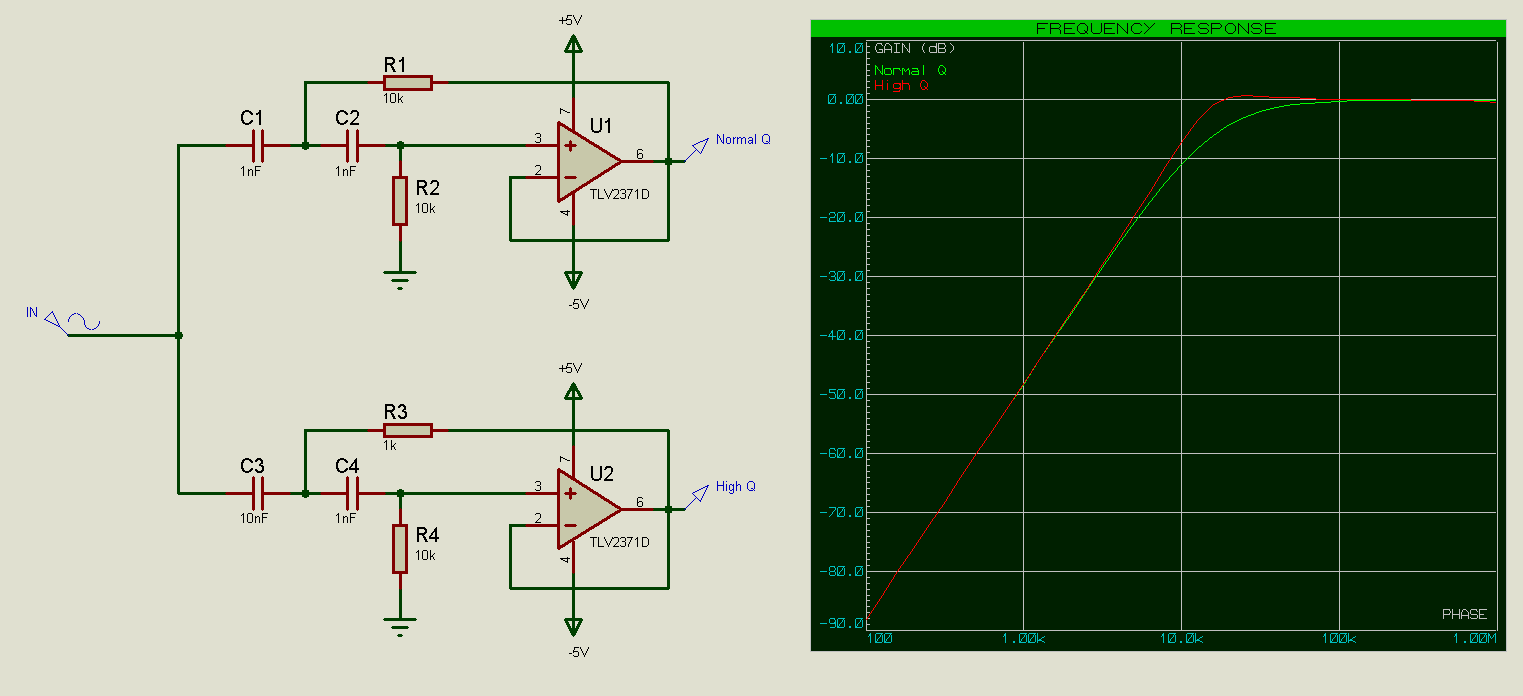
Calculs passe-haut
Les calculs sont les mêmes, à nouveau R2 = xR1 et C2=(1/x)C1.
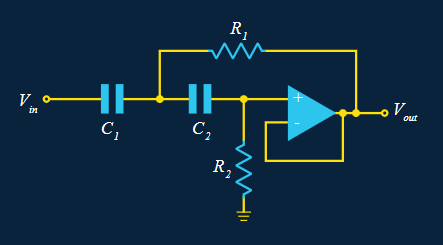
Pour x = 1, nous avons Q = 0,5 et pour x = 10, nous avons à nouveau Q = 0,91
Téléchargez les fichiers schémas Proteus utilisés dans cet article dans un seul ZIP.
Copyright Labcenter Electronics Ltd. 2024
Traduction française
Copyright Multipower France 2024
